To prove the identity: (1+cscθ−cotθ​)/(1+cscθ+cotθ) = cscθ−cotθ

Posted on Posted in Blog, Explainer Articles No Comments
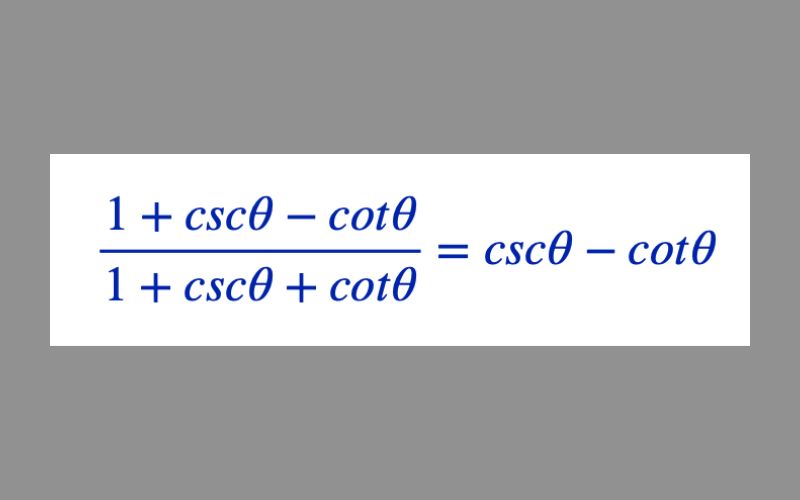
To prove the identity: (1+cscθ−cotθ​)/(1+cscθ+cotθ) = cscθ−cotθ

Introduction:

Trigonometry, the branch of mathematics that deals with the relationships between the angles and sides of triangles, often presents us with intriguing identities. One such identity that we’ll unravel in this blog post is:

1+csc⁡θ−cot⁡θ1+csc⁡θ+cot⁡θ=csc⁡θ−cot⁡θ

Let’s embark on a journey of proof, step by step, to demystify this seemingly complex trigonometric expression.

Step 1: Setting the Stage with LHS

We begin with the Left-Hand Side (LHS) of the equation:

LHS=1+csc⁡θ−cot⁡θ1+csc⁡θ+cot⁡θ

Step 2: Leveraging Trigonometric Identities

To simplify the expression, we tap into the rich world of trigonometric identities. Specifically, we employ the identity 1=csc⁡2θ−cot⁡2θ in the numerator:

LHS=csc⁡2θ−cot⁡2θ+csc⁡θ−cot⁡θ1+csc⁡θ+cot⁡θ

Step 3: Factoring the Numerator

The expression is now ready for some algebraic finesse. We factor the numerator using the identity

a2−b2=(a+b)(a−b)

LHS=(csc⁡θ+cot⁡θ)(csc⁡θ−cot⁡θ)+csc⁡θ−cot⁡θ1+csc⁡θ+cot⁡θ

Step 4: Taking Common Term Out

A key move in trigonometric proofs is often taking common factors. Here, we skillfully extract csc⁡θ−cot⁡θ from the numerator:

LHS=(csc⁡θ−cot⁡θ)(csc⁡θ+cot⁡θ+1)1+csc⁡θ+cot⁡θ

Step 5: Cancelling the Common Factor

With a common factor identified, we simplify further by canceling it out from both the numerator and denominator:

LHS=csc⁡θ−cot⁡θ1

If you’d like personalized assistance with trigonometry or other math topics, consider signing up for tutoring. 

Leave a Reply

Your email address will not be published. Required fields are marked *

*